3 Ex 2024
Problem 1: Pseudocode
Let \(A\) be the adjacency matrix representation of a directed graph \(G\) with \(n\) nodes. A node \(u\) is called balanced if the in-degree and out-degree of the nodes are equal. Let \(N_A\) be the amount of balanced nodes in the graph \(G\).
- Describe an algorithm
CountBalancedin pseudocode, that computes \(N_A\) in optimal asymptotic time. - Analyse the run-time of
CountBalancedand show that it is optimal.
Problem 2: Heaps
In this problem we look at binary Minheaps and carry out depth first search starting form the root, considering two variants:
incrDS: We visit the children of a node in increasing order, sorted w.r.t. the keysdecrDS: We visit the children of a node in decreasing oder, sorted w.r.t. the keys
Consider the following Min-Heap represented as an array \(H[1..10]\):
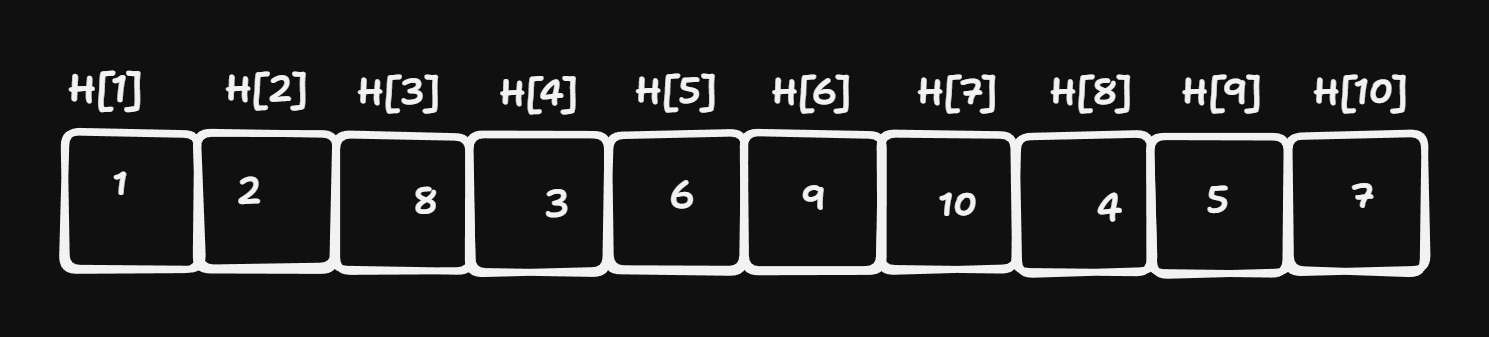
heap Provide the keys in the order that they are visited by
decrDS:Key-order: …
In the above heap
incrDStraverses the keys in a globally increasing order, i.e. it effectively ‘sorts’ the elements. Therefore we try to construct the following “sorting” algorithm:Let \(A[1..n]\) be an array with \(n\) keys. (You may assume that the keys are distinct).
- Transform \(A\) into a Min-Heap array representation
- Traverse \(A\) with
incrDSand output the elements in the order that they are visited
Prove that this algorithm can not always sort correctly. Provide a short analysis on the run-time of this algorithm.
Problem 3: Hashing
Consider the following hash table of size 13:

hash 1 You can assume that each empty cells corresponds to \(\bot\).
We consider first open hashing with hash function \(f\), defined as:
\[f(k) := 3k + 2 \mod 13\]
and we use linear search. Insert the elements 1, 2, 3, 4, 5 in this order in the provided table.
Consider another hash table of size 10:
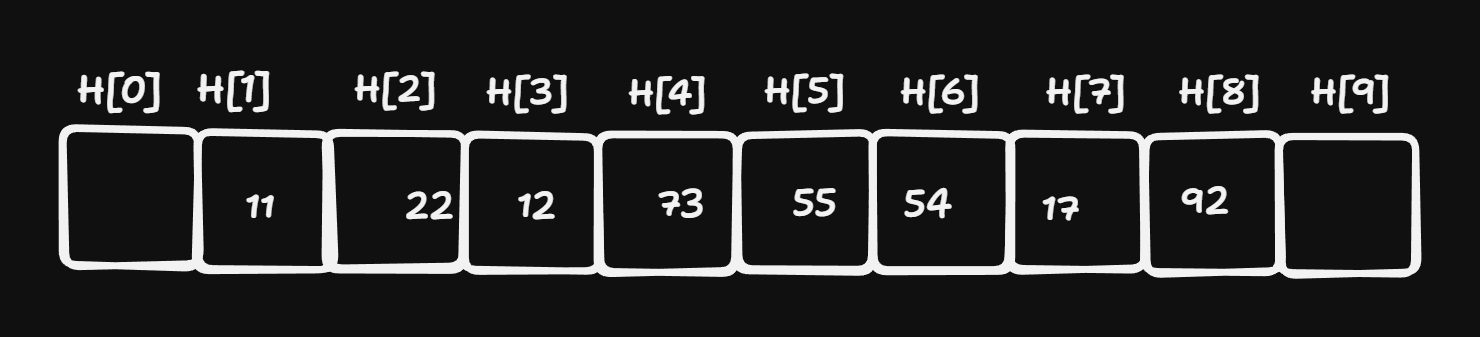
hash 2 We again use open hashing this time with the hashing function \(g\) defined as:
\[g(k) := k\mod 10\]
Delete the element 22 and provide the state of the hash table after this operation:
Problem 4: \(\mathcal{O}\)-Notation and Code Analysis
for each of the following cases provide a function \(f: \mathbb{N} \to \mathbb{R}\) that satisfies the given asymptotic constraints:
- \(f \in \omega \left( \frac{\log x}{\log \log x}\right)\) and \(f \in \omicron(\log x)\)
- \(f \in \omega(\sqrt[3]{m})\) and \(f \in \omicron\left(\frac{m}{\log m}\right)\)
- \(f \in \omega(\log t!)\) and \(f \in\omicron(t^2)\)
Solve the following recurive equations. For all the equations it holds that \(T(n) = 1\) and \(n\leq 1\). Assume for simplicity that for all equations \(n\) is chosen s.t. divisions result without a rest.
- \(T(n) = T(n - 1) + 2n\). \(\Rightarrow\) \(\quad\quad T(n) \in \Theta\left(\quad \right)\)
- \(T(n) = n\cdot T(n - 1)\). \(\Rightarrow\) \(\quad\quad T(n) \in \Theta\left(\quad \right)\)
- \(T(n) = 16\cdot T(\frac{n}{2})\). \(\Rightarrow\) \(\quad\quad T(n) \in \Theta\left(\quad \right)\)
- \(T(n) = 2\cdot T(\frac{n}{4}) + n\). \(\Rightarrow\) \(\quad\quad T(n) \in \Theta\left(\quad \right)\)
Provide the run-time complexit of the follwoing pseudocode algorithms in \(\mathcal{\Theta}\) notation.
:
read(k) for i = 1 to k: j = k^2 while j > 1: j = j / 3:
read(t) k = 1 i = 1 while k <= t : i = i + 1 k = k + i:
def fun(n) : read(n) if n < 10^6 : return f(n / 2) i = 0 while i < n : i = i + 1 f(n / 2)
Problem 5: Short Proofs
Show or refute following propositions:
- Let \(T = (V, E)\) be an arbitrary \((a, b)\)-Tree. Then \(T\) is also a \((a, b + 1)\)-Tree
- For any weighted, undirected, connected graph \(G = (V, E)\) any shortest-path tree is a minimal spanning tree.
- For any \(n > 1000\) there is a binary search tree that stores \(n\) keys \(\{1, \ldots, n\}\)
Problem 6: Induction
For a set \(X\), \(\mathcal{P}(A)\) is the set of all subsets of \(X\), called the power set.
Shows via mathematical induction that:
\[\text{for any set } X \text{ s.t. } |X| = n \text{ it holds that } |\mathcal{P}(X)| = 2^n\]
Problem 7: Graphs
Consider the following graph \(G\):
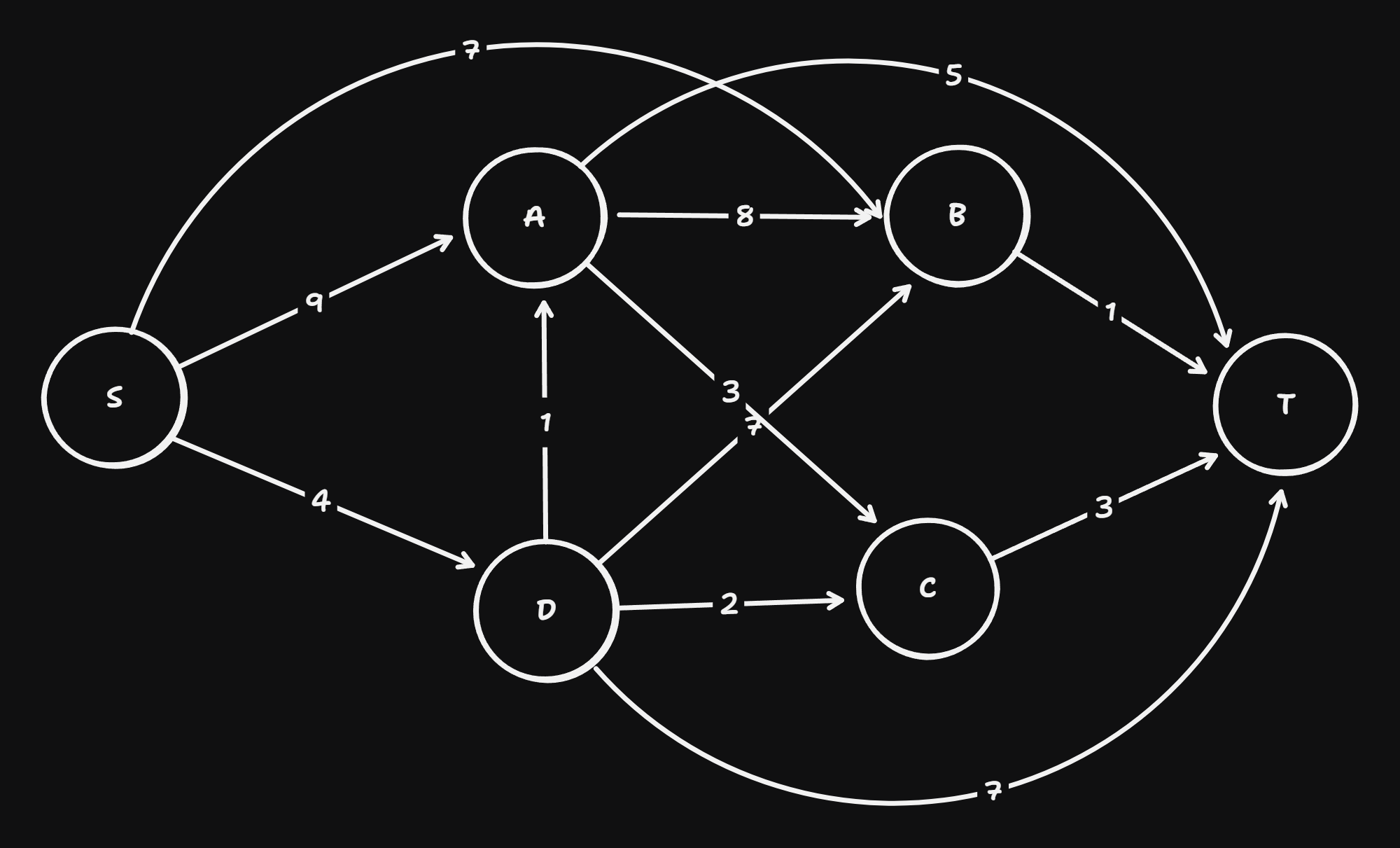
graph-1 Carry out the Dijkstra algorithm to find the shortest paths starting from the start node \(S\).
Provide each (Predecessor, Distance)-combination that is assigned to the node \(T\) by the algorithm:
provide the adjacency field representation of the following graph (CSR). Use the 1 as the smallest index and sort the neighbours in increasing order w.r.t. the index.
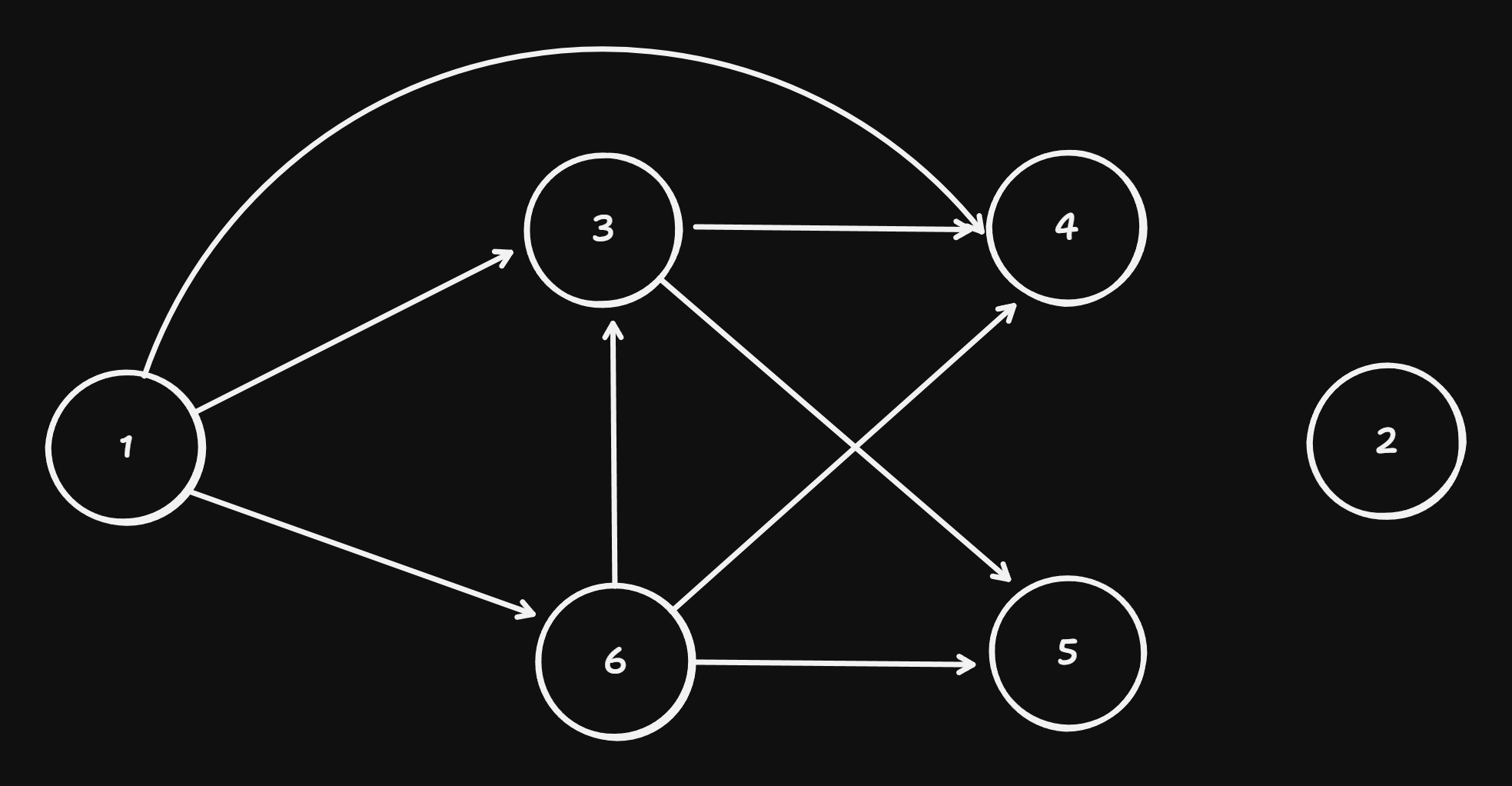
graph-2 Describe in pseudocode how the k-th neighbor of the i-th node is represented in the adjacency-field representation, using 1 as the smallest index. Name the invariants in the code that guarantee that required entry exists in the data structure. Provide the asymptotic analsysis of the \(\Theta\) run-time of the algorithm.