3 Arrays
An array is a contigious sequence of memory cells.
3.1 Bounded Arrays
Bounded arrays have fixed size and are an efficient data structure.
- Size must be known during compile time and is fixed.
- Its memory location in the stack allows many compiler optimizations.
3.2 Unbounded Arrays
The size of an unbounded array can dynamically change during run-time. From the user POV it provides the same behaviour as a linked list.
It allows the operations:
pushBack(e: T): insert an element at the end of the arraypopBack(e: T): remove an element at the end of the array
Memory Management
allocate(n): request a \(n\) contigious blocks of memory words and returns the address value of the first block. This we have the memory blocks: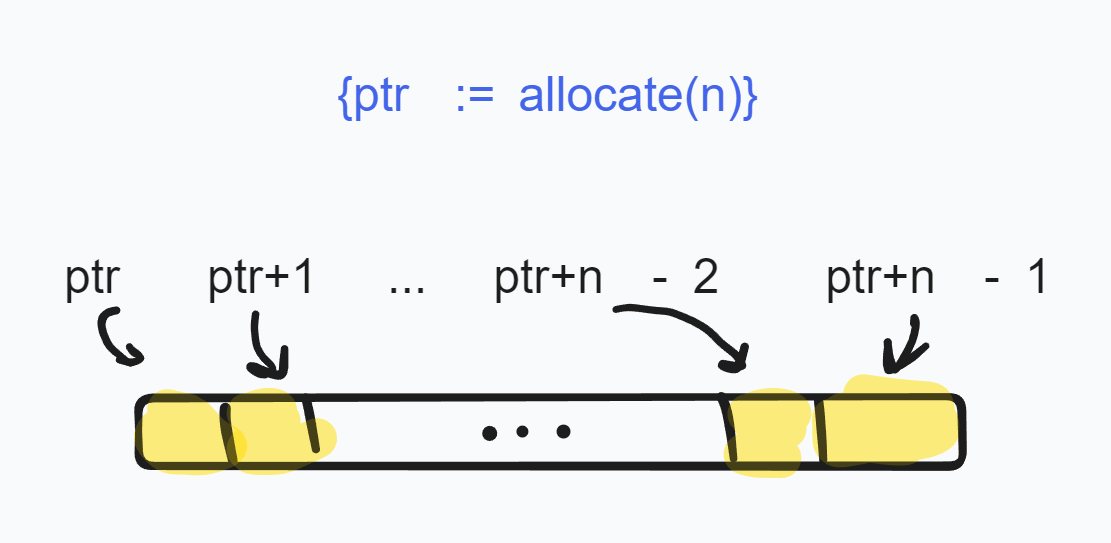
array memory allocation where
ptr + iaddresses are determined by pointer arithmetic.dispose(ptr)marks the memory address value held inptras free, effectively deleting the object held there.
In general, the allocated memory can’t grow dynamically during life time, since the immediate memory block after the last one might get unpredictably occupied \(\Rightarrow\) If we need a new memory block of size \(n' > n\), we must allocate a new block, copy the old block contents, and finally free it.
Implementation
First we consider a slow variant:
Class UArraySlow<T>:=
c := 0 : Nat // capacity
b : Array[0..c-1]<T> // the array itself
pushBack(el : T) : void :=
// c++
// allocate new array on heap with new capacity
// copy elements over from the old array
// insert el at the last location
popBack() : void :=
// analagousProblem: \(n\) pushBack operations require \(1 + \dots + n \in \mathcal{O}(n^2)\) time \(\Rightarrow\) slow.
Solution:
Unbounded Arrays with Extra Memory
Idea: Request more memory than initial capacity. Reallocate memory only when array gets full or too empty:
Algorithm design principle: make common case fast.
Class UArray<T> :=
c := 1 : Nat // capacity
n := 0 : Nat // number of elements in the array
//invariant n <= c < k*n || (n == 0 && c < 2)
b : Array[0..c-1]<T>
// Array access
Operator [i : Nat] : T :=
assert(0 <= i < n)
return b[i]
// accessor method for n
Function size() : Nat := return n
Procedure pushBack(e : T) :=
if n == c :
reallocate(2*n) // see definition below
b[n] := e
n++
// reallocates a new memory with a given capacity c_new
Procedure reallocate(c_new : Nat) :=
c := c_new
b_new := new Array[0..c_new - 1]<T>
//copy elements over to new array
for (i = 1 to n - 1) :
b_new[i] := b[i]
dispose(b)
b := b_new
Procedure popBack() :=
// don't do anything for empty arrays
assert n > 0
n--
if 4*n <= c && n > 0 :
reallocate(2*n)