4  Blatt 5

Aufgabe 3 (Sortieren)

Matrikel Nr: 3650174

Insertion Sort

Mit der folgenden Python Implementierung fuer Insertion-sort wird nach jedem Insert der Zustand des Arrays ausgegeben:

def insertion_sort(a) :
    n = len(a)
    # invariant: sorted a[0..i]
    for i in range(1, n) :
        # insert i in the right position
        j = i - 1
        el = a[i]
        while el < a[j] and j > 0 :
            a[j + 1] = a[j]
            j = j - 1
        # el >= a[j] or j == 0
        if el < a[j] : # j == 0
            a[1] = a[0]
            a[0] = el
        else : # el >= a[j] 
            a[j + 1] = el
        print("after insertion ", i, ": ", a)
    return a

insertion_sort([3, 6, 5, 0, 1, 7, 4])

after insertion  1 :  [3, 6, 5, 0, 1, 7, 4]
after insertion  2 :  [3, 5, 6, 0, 1, 7, 4]
after insertion  3 :  [0, 3, 5, 6, 1, 7, 4]
after insertion  4 :  [0, 1, 3, 5, 6, 7, 4]
after insertion  5 :  [0, 1, 3, 5, 6, 7, 4]
after insertion  6 :  [0, 1, 3, 4, 5, 6, 7]

[0, 1, 3, 4, 5, 6, 7]

Merge Sort

Siehe Abbildung:

merge sort

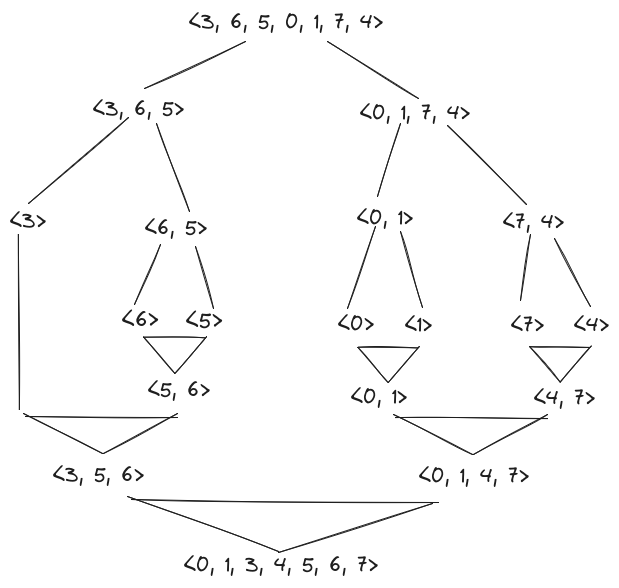
Quick Sort

1st call on 365017:

\[\begin{align*} &\overset{i}{3}65017\overset{j}{4} \tag{p = 2} \\ \Rightarrow &\overset{i}{3}650\overset{j}{1}74 \tag{iterate i, j} \\ \Rightarrow &\boxed{3}650\boxed{1}74 \tag{swap 3, 1} \\ \Rightarrow &1\overset{i}{6}5\overset{j}{0}374 \tag{iterate i, j} \\ \Rightarrow &1\boxed{6}5\boxed{0}374 \tag{swap 6, 0} \\ \Rightarrow &10\overset{i,j}{5}6374 \tag{iterate i, j} \\ \Rightarrow &1\overset{j}{0}|\overset{i}{5}6374 \tag{end} \end{align*}\]

2nd level call 1 on 10:

\[\begin{align*} &\overset{i}{1}\overset{j}{0} \tag{p = 1} \\ \Rightarrow &\overset{j}{0}\overset{i}{1} \tag{iterate i, j; swap 1, 0; end} \end{align*}\]

2nd level call 2 on 56374:

\[\begin{align*} &\overset{i}{\boxed{5}}637\overset{j}{\boxed{4}} \tag{p = 5, iterate, swap 5, 4} \\ \Rightarrow &4\overset{i}63\overset{j}75 \tag{iterate} \\ \Rightarrow &4\overset{i}{\boxed{6}}\overset{j}{\boxed{3}}75 \tag{swap} \\ \Rightarrow &4\overset{j}{3}|\overset{i}{6}75 \tag{end} \end{align*}\]

3rd level call 1 on 43:

\[\begin{align*} &\overset{i}{4}\overset{j}{3} \tag{p = 4} \\ \Rightarrow &\overset{j}{3}\overset{i}{4} \tag{iterate i, j; swap 4, 3; end} \end{align*}\]

3rd level call 2 on 675:

\[\begin{align*} &\overset{i}{6}7\overset{j}{5} \tag{p = 6} \\ \Rightarrow &\overset{i}{\boxed{6}}7\overset{j}{\boxed{5}} \tag{iterate; swap} \\ \Rightarrow &5\overset{ij}{7}6 \tag{iterate} \\ \Rightarrow &\overset{j}{5}|7\overset{i}{6} \tag{end} \end{align*}\]

4th level last call on 76:

\[\begin{align*} &\overset{i}{7}\overset{j}{6} \tag{p = 7} \\ \Rightarrow &\overset{j}{6}\overset{i}{7} \tag{iterate i, j; swap 7, 6; end} \end{align*}\]

alltogether:

3 6 5 0 1 7 4
1 0|5 6 3 7 4
0 1|4 3|6 7 5
   |3 4|5|7 6
         |6 7

=> output: 0 1 3 4 5 6 7