Zettel 02
Aufgabe 2
Idee: Vertausche erstes 0 und letzets 1 und interpretiere die Anzahl der 1’en auf dem Band als das Ergebniss.
Seien z.B.: \(n := 4, m := 3\). Dann gilt:
\[\begin{align*} 4 + 3 &\equiv 1111\fbox{0}11\fbox{1}0 &&\tag{Kodieren der Eingabe} \\ &\Rightarrow 1111\fbox{1}11\fbox{0}0 &&\tag{Vertausche erstes 0 und letztes 1} \\ & \equiv 7 &&\tag{Dekodieren der Ausgabe} \end{align*}\]
Die TM - gegeben durch den folgenden Uebergangsgraph und Uebergangstabelle (Siehe Figure 2 und Figure 1) - realisiert diese Berechnung:

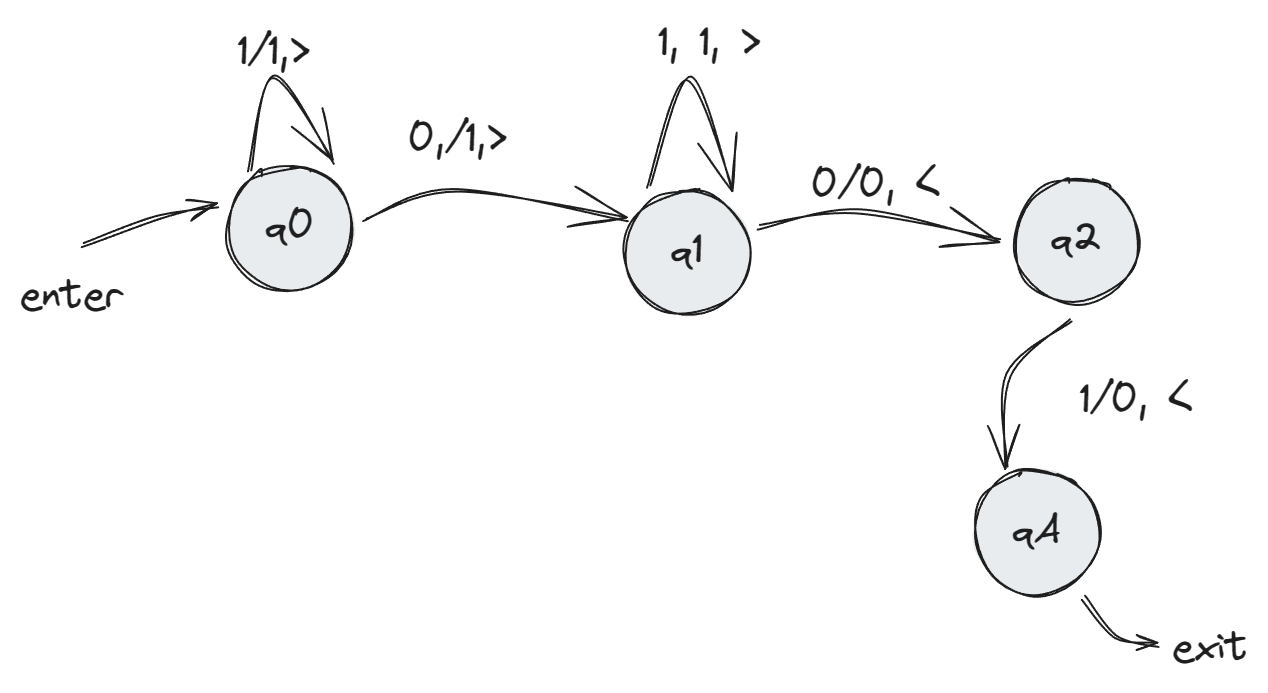
Begruendung/Erklaerung der Vorgehensweise dieser TM:
- \(q_0\): Das ist der initialer Zustand. Lese 1’en und bewege den Kopf rechts bis erstes 0 gefunden wird. Ersetze diesen 0 durch einen 1, bewege den Kopf rechts und gehe zum Zustand \(q_1\) ueber
- \(q_1\): Erstes 0 wurde gefunden und durch 1 ersetzt. Lese 1’en und bewege den Kopf rechts bis der zweite 0 gefunden wird. Das ist das Ende der Eingabe. Bewege den Kopf ein mal links zurueck und gehe zum Zustand \(q_2\) ueber.
- \(q_2\): Der Kopf steht auf den letzten 1 der Eingabe. Ersetze diesen 1 durch einen 0 und bewege den Kopf ein mal links. Da das Ziel erreicht wurde (vertauschen der ersten 0 und letzten 1) gehe zum Zustand \(q_A\) ueber.
- \(q_A\): Das ist der akzeptierende Zustand. Falls die Eingabe gueltig ist haelt der TM im Zustand \(q_A\) mit dem richtigen Ergebniss auf dem Band.
Folgendes Programm realisiert diese TM auf dem TM simulator, wobei 0’s durch blanks ersetz wurden, und letzte Bewegung ‘hold’ statt ‘links’ ist. (Das Programm ist auch als txt datei im Zip enthalten)
//TM machine to add two numbers n and m
//Input: string of n 1's and a string of m 1's seperated my a blank
//Output: string of m + n 1's
//Example: Input: "1111 111"
// Output: "1111111"
name: add two numbers
init: q0
accept: qA
q0,1
q0,1,>
q0,_
q1,1,>
q1,1
q1,1,>
q1,_
q2,_,<
q2,1
qA,_,-Alternativ: link zur realisierung der TM auf der Webseite.
Aufgabe 3
Eine sprache fuer lineare Gleichungssysteme kann z.B. durch folgende EBNF-syntaxbeschreibung definiert werden:
\[\begin{align*} \langle Gleichungssystem\rangle &::= \langle Gleichung\rangle\{\underline{\backslash n} \langle Gleichung\rangle\} \\ \langle Gleichung\rangle &::= [\langle Zahl\rangle]\underline{x}\langle Index\rangle\{\langle Vorzeichen\rangle[\langle Zahl\rangle]\underline{x}\langle Index\rangle\}\underline{=}\langle Zahl\rangle \\ \langle Vorzeichen \rangle &::= \underline{-} | \underline{+} \\ \langle Zahl\rangle &::= \langle Ersteziffer\rangle \{\langle Ziffer\rangle \} \\ \langle Ersteziffer\rangle &::= \underline{1} | \underline{2} | \underline{3} | \underline{4} | \underline{5} | \underline{6} | \underline{7} | \underline{8} | \underline{9} | \\ \langle Ziffer\rangle &::= \underline{0} | \langle Ersteziffer\rangle \\ \langle Index\rangle &::= \underline{_0} | \langle Subzahl\rangle \\ \langle Subzahl\rangle &::= \langle Erstesubziffer\rangle \{\langle Subziffer\rangle \} \\ \langle Erstesubziffer\rangle &::= \underline{_1} | \underline{_2} | \underline{_3} | \underline{_4} | \underline{_5} | \underline{_6} | \underline{_7} | \underline{_8} | \underline{_9} | \\ \langle Subziffer\rangle &::= \underline{_0} | \langle Erstesubziffer\rangle \end{align*}\]
Die Anforderung “Die Anzahl der Variablen ist gleich der Anzahl der Gleichungen” ist eine Beschreibung die von dem Kontext des Erzeugten Wortes abhaengt - gueltige Gleichungssysteme duerfen beliebige Anzahl an Variablen haben. Da mit EBNF nur kontextfreie Sprachen definiert werden koennen ist diese Anforderung nicht umsetzbar.