Zettel 03

Aufgabe 2

2.1

Folgendes Program loesst das problem (auch im zip als potenz.cc enthalten)

#include "fcpp.hh"

int quadrat (int x)
{
  return x*x;
}

int potenz(int x, int n)
{
    return cond(n == 0, 
            1, 
            cond(n % 2 == 0, 
                quadrat(potenz(x, n / 2)), 
                x * potenz(x, n - 1)));
}


int main(int argc, char** argv)
{
    return print(potenz(
      readarg_int(argc, argv, 1), 
      readarg_int(argc, argv, 2)));
}

Argumente muessen in der Konsole eingegeben werden, z.B.:

$ ./potenz 4 3
81

Aufgabe 3

3.1

Folgendes Program realisiert die rekursive Berechnung der Binomialkoeffizienten (auch im Zip als binomial.cc enthalten):

#include "fcpp.hh"

int binomial(int n, int k)
{
    return cond(k == 0 || k == n, 
            1,
            binomial(n - 1, k - 1) + binomial(n - 1, k));
}

int main(int argc, char** argv)
{
    return print(binomial(
        readarg_int(argc, argv, 1),
        readarg_int(argc, argv, 2)));
}

Wir haben das Program auf verschieden Werte \(n\) und \(k\) getestet (zusammen mit der time Funktion fuer Messung der Laufzeit) und die Ergebnisse in der folgenden Tabelle zusammengefasst:

Note

Specs des Systems auf der wir getestet haben:

PC: ThinkCentre M700
Processors: 4 × Intel® Core™ i5-6400 CPU @ 2.70GHz
Memory: 15,5 GiB of RAM

Befehl	Ergebniss	Laufzeit (real)
`time ./binomial 1 0`	1	`real 0m0,004s`
`time ./binomial 1 1`	1	`real 0m0,002s`
`time ./binomial 3 2`	3	`real 0m0,002s`
`time ./binomial 10 4`	210	`real 0m0,004s`
`time ./binomial 20 13`	77520	`real 0m0,007s`
`time ./binomial 32 15`	565722720	`real 0m3,519s`
`time ./binomial 36 13`	-1984177696	`real 0m13,791s`

Wie aus der Tabelle zu sehen ist, ist die Laufzaut \(>10s\) fuer die Berechnung time ./binomial 36 13 jedoch mit dem falschen Ergebniss -1984177696 statt das richtige \(\binom{36}{13} = 2310789600\). Wir erklaeren dieses Phaenomen in der folgenden Teilaufgabe.

3.2

Fuer \(n = 34\), \(k = 18\) liefert das Program

$ ./binomial 34 18
-2091005866

im Gegensatz zu dem erwarteten mathematischen Ergebniss \(\binom{34}{18} = 2203961430\).

Dieser ‘Fehler’ liegt an der 32 bit 2er Komplement Darstellung des Datentyps int auf dem Computer. Darunter koennen eine endliche Anzahl von int Zahlen dargestellt werden, die im Bereich \([-2^{31}, 2^{31} - 1] = [-2147483648, 2147483648]\) liegen. Das mathematische Ergebnis liegt also ausserhalb des darstellbaren Bereiches mit \(2203961430 > 2147483648\).

Da, unter der 2er Komplement Darstellung der MSB (Most Significant Bit) den Bereich der Negativen Zahlen representiert kann die Addition zweier groessen Zahlen, deren Ergebniss ausserhalb des darstellbaren Bereiches liegt wieder bei dem negativen Bereich landen, aehnlich wie Modulorechnung. Das wird als overflow bezeichnet.

3.3

Sei \(A_{n, n} = \alpha = A_{n, 0}\) und \(\beta := \text{Die konstanten Kosten der Addition}\). Dann gilt:

\[\begin{align*} &A_{n, k} = A_{n-1, k-1} + A_{n-1, k} + \beta \tag{Rekursive Beziehung des Rechenaufwands} \\ &A_{n, 0} = \alpha = A_{n, n} \end{align*}\]

Da die rekursive Beziehungs des Rechenaufwands eine aehnliche Beziehung wie die Binomialkoeffizienten erfuellen koennen diese in einem paskalschen Dreieck wie folgt eingetragen werden (Siehe Figure 1)

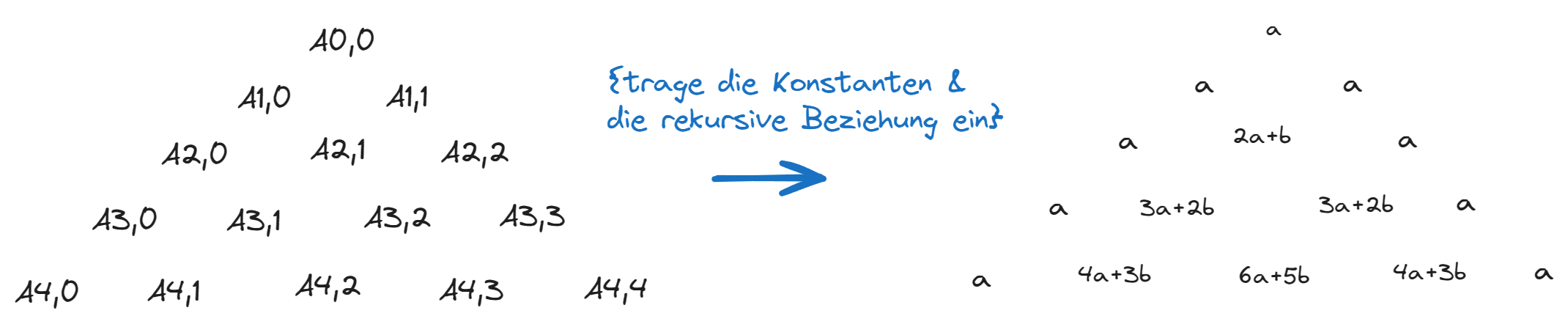
Betrachten wir nur die Koeffizienten von \(\alpha\) und \(\beta\) seperat so erhalten wir folgende paskalschen Dreiecke (Siehe Figure 2)

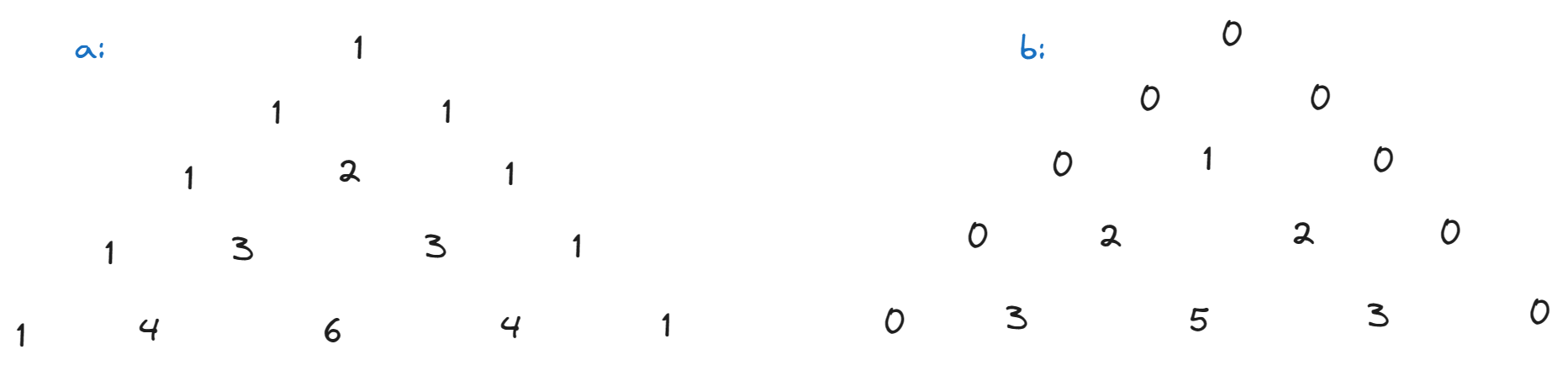
Von diesen Figuren ist es leicht zu sehen, dass \(\alpha_{n, k} = B_{n, k}\) und \(\beta_{n, k} = B_{n, k} - 1\), wobei \(\alpha_{n, k}, \beta_{n, k}\) die Koeffizienten von \(\alpha\) bzw. \(\beta\) sind bzgl der Rechenaufwands \(A_{n, k}\).

Somit erhalten wir:

\[A_{n, k} = B_{n, k}\alpha + (B_{n,k} - 1)\beta\]

Formaler Beweis:

Fuehre die Variablentransformation \(\tilde{A}_{n, k} := \frac{A_{n, k} + \beta}{\alpha + \beta}\). Dann erhalten wir die folgende rekursive Gleichung:

\[\begin{align*} &\tilde{A}_{n, k} = \tilde{A}_{n-1, k-1} + \tilde{A}_{n-1, k} \\ &\tilde{A}_{n, 0} = 1 = \tilde{A}_{n, n} \end{align*}\]

Das ist genau die Definition des Binomialkoeffizientes \(B_{n, k}\). Somit gilt:

\[\begin{align*} \tilde{A}_{n, k} &= B_{n, k} \\ \Rightarrow A_{n, k} &= (\alpha + \beta)\tilde{A}_{n, k} - \beta \\ &= (\alpha + \beta)B_{n, k} - \beta \quad \blacksquare \end{align*}\]

3.4

Folgend geben wir die iterative Implementierung der Binomialkoeffizienten anhand einer tail-rekursiven Implemenierung der Fakultaet-funktion an (auch im Zip als binomial_fast.cc erhalten):

#include "fcpp.hh"

//iterative Implementierung der Fakultaetsfunktion durch Tail-recursion 
// mit fakit und fak
int fakit(int res, int n)
{
    return cond(
        n > 1,
        fakit(res * n, n - 1),
        res
    );
}

int fak(int n)
{
    return fakit(1, n);
}

int binomial_fast(int n, int k)
{
    return fak(n) / (fak(k) * fak(n - k));
}

int main(int argc, char** argv)
{
    return print(binomial_fast(
        readarg_int(argc, argv, 1),
        readarg_int(argc, argv, 2)));
}

Da, die Implementierung von Fakultaet fak \(\mathcal{O}(n)\) ist , binomial_fast nur drei mal fak aufruft und nur zwei weitere Basisoperationen verwendet - eine Multiplikation und eine Division - hat diese Implementierung eine Laufzeitkomplexitaet von \(\mathcal{O}(n)\).

Wir haben binomial und binomial_fast auf verschiedene Eingaben hinsichtlich Ausgaben und Geschwindigkeit getestet und die Ergebnisse in der folgenden Tabelle zusammengefasst (Table 1):

Table 1: `binomial` vs `binomial_fast`
Befehl	Ergebniss	Laufzeit (real)
`time ./binomial 10 4` `time ./binomial_fast 10 4`	`210` `210`	`real 0m0,004s` `real 0m0,004s`
`time ./binomial 11 6` `time ./binomial_fast 11 6`	`462` `462`	`real 0m0,005s` `real 0m0,005s`
`time ./binomial 13 10` `time ./binomial_fast 13 10`	`286` `88`	`real 0m0,005s` `real 0m0,004s`
`time ./binomial 20 13` `time ./binomial_fast 20 13`	`77520` `-2`	`real 0m0,006s` `real 0m0,002s`
`time ./binomial 27 15` `time ./binomial_fast 27 15`	`17383860` `0`	`real 0m0,123s` `real 0m0,004s`
`time ./binomial 32 15` `time ./binomial_fast 32 15`	`565722720` `-3`	`real 0m3,519s` `real 0m0,004s`
`time ./binomial 34 19` `time ./binomial_fast 34 19`	`1855967520` `0`	`real 0m11,689s` `real 0m0,002`
`time ./binomial 36 13` `time ./binomial_fast 36 13`	`-1984177696` `0`	`real 0m15,388s` `real 0m0,004s`
`time ./binomial 39 23` `time ./binomial_fast 39 23`	`-943444674` `core dumped`	`real 3m47,934s` `real 0m0,086s`

Da binomial_fast eine lineare Laufzeitkomplezitaet hat bleibt die Laufzeit c. .004s fuer alle Eingaben.

Im Gegensatz waechst die Laufzeit von binomial proportional zu dem mathematischen Wert \(B_{n, k}\) fuer Eingaben \(n\) und \(k\). Somit ist die Laufzeit sehr hoch fuer grosse Werte von \(B_{n, k}\).

Wie aus der Tabelle zu sehen ist, gibt es bereits ab \(n = 27, k = 15\) einen Unterschied und fuer hoehere Werte wie \(n = 34, k = 19\) oder \(n = 36, k = 13\) unterscheiden sich die Laufzeiten um mehr als 10s. Fuer \(n = 39, k = 23\) ist die Laufzeit von binomial sogar fast 4 minuten, wobei binomial_fast immer noch bei ~0.004s bleibt.

3.5

Fuer diese Teilaufgabe verwenden wir wieder die obige Tabelle Table 1. Fuer die ersten zwei Zeilen, also fuer \(n = 10, k = 4\) und \(n = 11, k = 6\) liefern beide Programme die richtige mathematische Ergebnisse \(\binom{10}{4} = 210\), bzw. \(\binom{11}{6} = 462\). Jedoch liefert binomial_fast bereits ab der dritten Zeile, also fuer \(n = 13, k = 10\) ein falsches Ergebnis, wobei binomial bis der 7en Zeile, d.h fuer \(n = 34, k = 19\) richtige Ergebnisse liefert.

Wie in der Teilaufgabe 3.3 erklaert wurde, gibt es das sogenannte Phaenomen “overflow” fuer den Datentyp int. Die Fakultaetsfunktion waechst sehr schnell und hat bereits fuer die Eingabe 13 den Wert \(13! = 6 227 020 800 > 2 147 483 647 = 2^{31} - 1\). Somit fuehrt bereits fak(13) zu einem overflow. Da, die Implementierung vonbinomial_fast die Funktion fak benutzt, liefert dieses Program fuer Eingaben \(n \geq 13\) ein falsches Ergebnis.