Week 1

Published

April 15, 2025

VL 1 - 15.04.25

  • Heico: Rundmails, Pruefungen
  • MaMPF: VL Skript & Videos, Uebungen
  • Discord: Fragen, Teamfindung
  • Muesli: Uebungspunkte
  • Algorithms and programming with python (python crashcourse next week)
  • website

lecture notes:

Algorithms and Data Structures

  • Algorithmus:

    1. loest eint bestimmtes (wohldefiniertes) Problem - “Spezifikation”
    2. loest das Problem in endlich vielen Schritten - “Komplexitaetstheorie”
    3. Alle Schritte sind elementar (Bekannte einfache Subalgorithmen)

  • Problem - Spezifikation:

    • formale Beschreibung der Aufgabe
    • enthaelt nicht die Loesung

  • Vorbedingugen: Notwendiger Zustand der “Welt”, damit der Algorithmus andwendbar ist. (Anforderungen and die Eingaben, evts, auch andere Umbegung)

  • Nachbedingen: Zustand der “Welt” am Ende des Algoirhtmus.

  • Bsp: Quadratwurzel \(y = \sqrt{x}\)

    • Vorbedingung: \(x \in \mathbb{N}\), oder \(x \in \mathbb{R}^{\geq 0}\) oder \(x \in \mathbb{R}\), if \(y \in \mathbb{C}\)
    • Nachbedingung: \(y \cdot y == x\), falls Vorbedingung erfuellt, anderfalls, d.h. \(x \notin \mathbb{R}\), or \(x < 0\), dann Fehlermeldung:
    • \(x \in \texttt{string}\): Type error
    • \(x < 0\): Value error

  • Elementare Schritte:

    • pragmatische Definition: alles, was die Hardware, Programmierscprahe & Standartbibliothek schoin anbietet.
    • formale Definition: Theoretische informatik - spezifikation Elementarer Operationen.
      • Beispiel aus der Geometrie: Konstruktionen mit Zirkel und Lineal
        • Elementare Operationen:
          1. defniere inen Punkt: (a. beliebig, b. als Schnittpunkt)
          2. mit Zirkel Abstand zwischen zwei Punkte abgleichen
          3. mit Zirkel einen Kres um einen geg. Punkt schneiden
            1. Radius beliebig
            2. aus 2)
          4. Mit Lineal Gerade durch zwei Punkte zeichnen.

  • Theoretische Informatik:

    • Ziel der Theoretischen Informatik: mit moeglischst wenig Regeln (Elementare op.) moeglichst viele Algorithmen.
    • \(\lambda\)-Calculus
    • Recursive Functions Theory
    • Turing Machine Computability
    • While-computability
    • Ueberraschendes Theorem der Theoretischen Informatik: Die Menge der realisierbaren Algorithmen ist gleich bei allen Systemen (berechenbare Funktionen)
    • Church-Turing These: Es gibt kein maechtigeres Regelsystemen (model of computability).
    • while-programme:
      • addition einer Konstante
      • substraktion einer Konstante
      • nacheinander Ausfuehrung zwei Programme (Anweisungen)
      • while-schleife

VL 2 - 17.04.25

Minimal set of elementary operations

while-programs:

set of operations:

  • accesing a memory cell, read / write: X[i]

  • adding a constant \(c\) to a memory cell and storing the result in an arbitary cell: X[j] := X[i] + c

  • substracting a constant \(c\) from a memory cell: X[j] := X[i] - c

  • composition of programs: \(P\), \(Q\) programs, then \(P;Q\) is a program

  • while loop:

    while x[i] != 0 do
  P // an arbitrary Program
done

    in this definition such a while program is valid if x[i] eventually becomes 0. (otherwise, infinite loop => no algorithm)

  • theorem: with these Elementary operations, all Turing-computable functions can be computed.

  • example: addition of two cells

    • precondition: X[j] >= 0

    • poscondition: X[i]' == X[i] + X[j]

    • implementation:

      read(X[i]);
read(X[j]);
// X[j] >= 0 && X[i] + X[j] == X + Y
while X[j] > 0 do
  X[j] = X[j] - 1;
  X[i] = X[i] + 1 
done
// X[j] == 0

Around 1400 there was a disagreement about elementary operations. Two camps: Abacus-oriented vs Algorithm-oriented

  • Abacus-oriented: Roman numerals + abacus operations. (Abacus operations were extremely fast with roman numbers)
  • Algorithm-oriented: how to compute with indian number, pen and paper - based on the book of Al Quarismi.

1500 Adam Ries: “Rechnen auf der Federn und Linien” (Pen and Abacus)

Heute: pragmatic definition of elementary operations based on the capabilities of the CPU, or on the programming language level the basic operations of the programming language.

Data Structures

Definition: Storing data in a way that can be found easily and interpreted correctly.
Example: Consider sequence of bits: 1101,0110,0110,1100. The ‘meaning’ of this sequence depends on how
it is interpreted:

  • interpretation as a positive binary number.
  • interpretation as a binary integer => 2s complement.
  • interpreted as a sequence of 8-bit characters:
  • imterpreted as a floating point number according to the IEEE standard: S | EEEEE | MMMMMMMMMM

main point: same symbol can be interpreted in various ways, depending on the system.

  • programming languages: variables have associated types and the compiler or the interpreter determines what type it is and interprets this accordingly.
  • Files:
    • ending of the file .jpg
    • magic number in file”: 255 216 255
    • type standards for communication and Operating system.

Data-structure Triangle

data-triangle

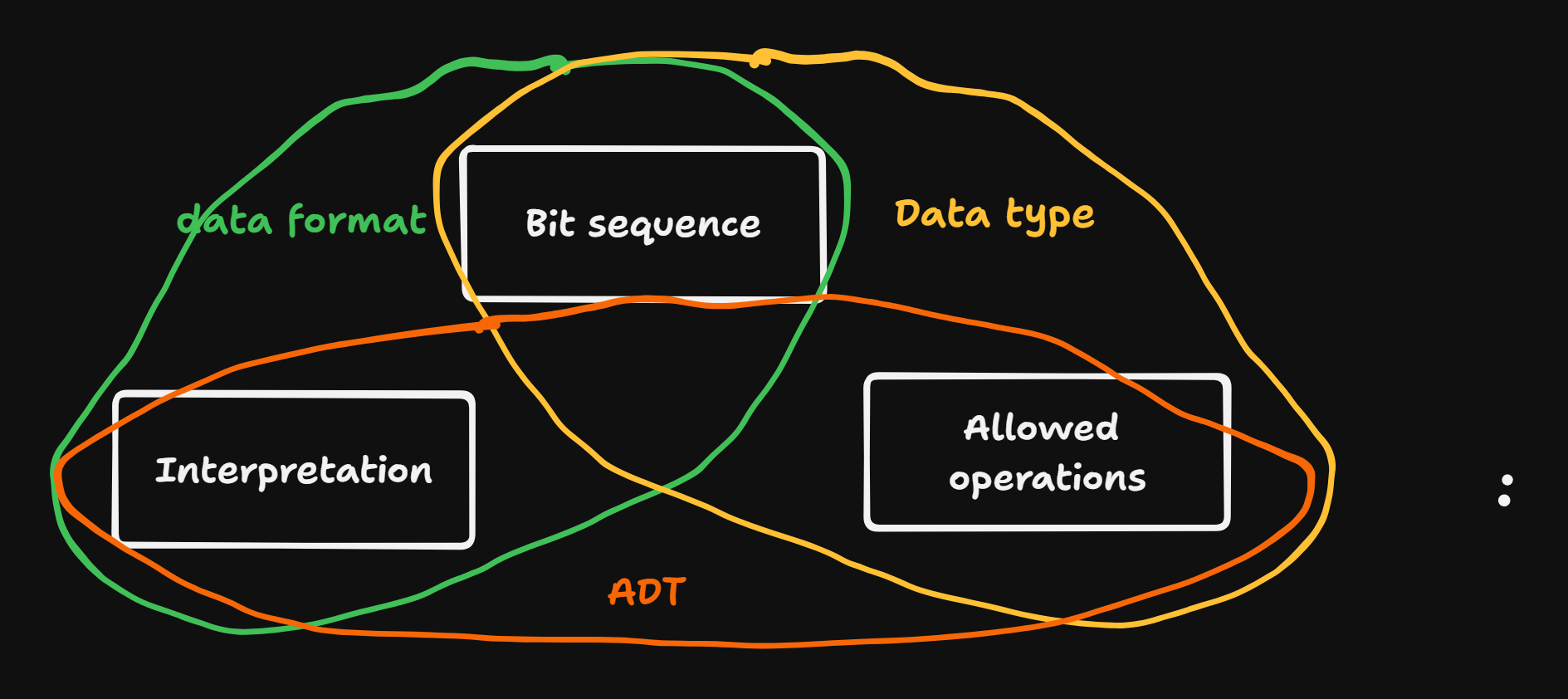
ADT: abstract data type = no implementation is given, no bit sequence is defined. Supported operations and range of values is defined.