Week 13

Published

July 8, 2025

VL 24 - 08.07.25

Connected Components

Searching and Identifying Connected Components

Idea: each component has a label (a running number) and an anchor (representative of the equivalence class)
Scan the nodes in increasing order, until a new anchor is found. This is a node whose connected component is not known
DFS or BFS starting from an anchor, in order to find the other nodes in the equivalence class.

Homework: Segmentation of a microscope image with connected components
how to represent additional properties of nodes and edges?
- visited[node]: was the node visited?
- anchor[node], label[node]: anchor and the label of the connected component to which the node belongs
- brightness[node]: the brightness of a pixel
- `distance[(node1, node2)]: shortest paths frmo node1 to node2
above are called ‘property maps’ via containers like arrays, dictionaries. It is a lightweight approach. A separate property map for each property.

First we will look at the recursive version

def connected_component(graph) : # graph given as an adjecency list
    labels = [None] * len(graph)
    anchors = [None] * len(graph)
    def visit(node, anchor):
        if anchors[node] is not None: return # already visited / known component
        labels[node] = labels[anchor]
        anchors[node] = anchor
        for neighbor in graph[node] :
            visit(neighbor, anchor)
    current_label = 0
    for node in range(len(graph)) :
        if labels[node] is not None: continue
        labels[node] = current_label
        visit(node, node) # a compnent is now complete
        current_label += 1
    return labels, anchors

Problem “Maximum Recursion Depth Exceeded” $\Rightarrow$ a variant with iteration and a stack DS:

def connected_components(graph):
    labels = [None] * len(graph)
    anchors = [None] * len(graph)
    current_label = 0
    for node in range(len(graph)) :
        if labels[node] is not None : continue
        stack = deque() # from collections
        stack.append(node)
        while len(stack) != 0 :
            new_node = stack.popright() # pop() in newer python
            if labels[new_node] is not None: continue
            labels[new_node] = current_label
            anchors[new_node] = node
            for neighbor in graph[new_node] : 
                if labels[neighbor] is not None: continue
                stack.append(neighbor)
        # end while: stack is now empty, DFS for the component is complete.
        current_label += 1 # proceed to the next label
    # end for: all components are complete
    return labels, anchors

Next problem we will take on is shortest path

Shortest Path

3 types of SP problems:
1. unweighted graph (ungewichtet): all edges are equally expensive: shortest path = the least number of edges $\Rightarrow$ BFS
2. weighted graph, all weights are positive ($w_{uv}> 0$), Path length = Sum of the weights $\Rightarrow$ Dijsktra Algorithm, or A* algorithm
3. weighted graph with arbitrary weights (positive and negative) $\Rightarrow$ length = sum of weights. Danger of an infinite loop when the sum of weights of a cycle is negative. solution: Bellman-Ford Algorithm (this algorithm terminates when a negative cycle is detected)

Example: negative cycle in Arbtrage-companies:

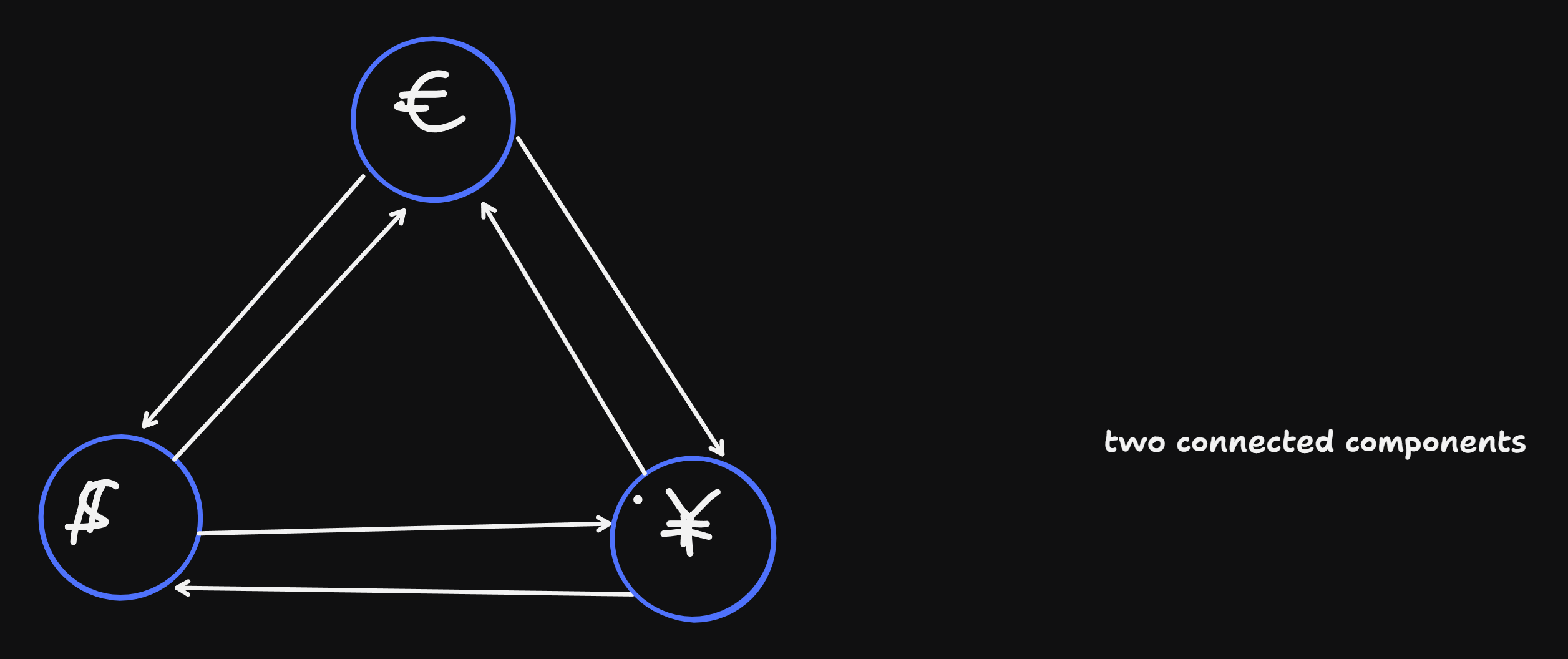
what happens:

we have x$,
- exhnage to Eu => y yen = $w_{\$eu}$ x$.
- exchange to Yen => z yen = w_{eu, yen}w_{$,eu} x $
- exhnage to $ => w_{yen, $} w_{eu, yen} w_{$, eu} x $
there is profit when w1w2w3 > 1
shortest paht: -log(x’) < -log(x) <=> -log(w1 * w2 * w3) < negative cycle

Now we need ne property maps for shortest paths. Each node knows it’s predecessor in the path $\Rightarrow$ parents[node]

def shortest_path(graph, start, target): # graph is undirected
    parents = [None] * len(graph)
    parents[start] = start
    queue = deque()
    queue.append(start)
    while len(queue) != 0 :
        node = queue.popleft()
        if node == target : break # success 
        for neighbor in graph[node] : 
            if parents[neighbor] is None :
                parents[neighbor] = node
                queue.append(neighbor)
    if parents[target] is None : 
        return None # start & target are in the same connected component
    path = [target]
    while path[-1] != start : # not yet finished
        path.append(parents[path[-1]])
    path.reverse() # target not 
    return path

Why doesn’t shortest path work with DFS?

VL 25 - 10.07.25

BFS (cont)

Why does BFS find the shortest path?

undirected & unweighted graph

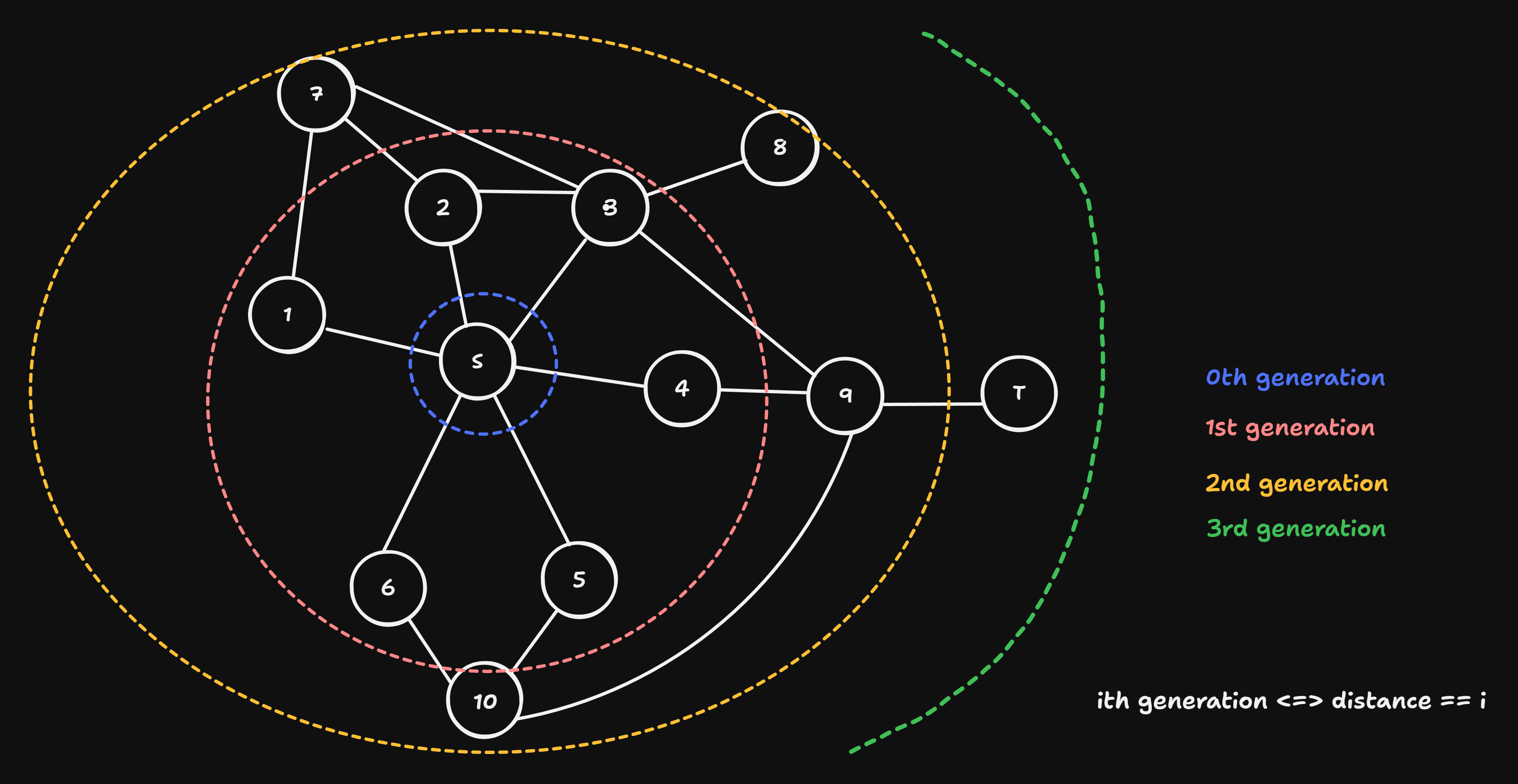
Obersvations:

BFS expands / propagates in phases around the start node.
BFS doesn’t only find the shortest path from start to target, but all shortest paths with length $l < \text{length}(\text{start}\rightsquigarrow\text{target})$ (shortest paths to all nodes that are closer to start than the target)

Shortest Paths in Weighted Graphs (Dijkstra & A* - Alg)

Edge weights represent the lenghts of edges $w_{uv} > 0$
Property maps: weights[(u,v)] with node pairs as keys

Alternatively adjacency matrix. Entries are weights of the edges:

\[ \begin{bmatrix} 0 & 4 & 7 \\ 4 & 0 & 2 \\ 7 & 2 & 0 \\ \end{bmatrix} \]

But we will use adjacency lists and property maps .

Idea: Replace the queue in BFS by a MinHeap (priority queue), where the priority of a node = length(start -> node). (in the lecture we had max heaps, but now we need a min heap - in python this is already the case in the module haepq ).

algorithm:

def dijkstra(graph, weights, start, target) :
    parents = [None] * len(graph) #
    heap = []
    heapq.heappush(heap, (0.0, start, start)) # 0.0 = priority, start = current, start = parent
    while len(heap) != 0 :
        length, node, parent = heapq.heappop(heap)
        if parents[node] is not None : continue 
        parents[node] = parent
        if node == target: break # success 
        for neighbor in graph[node] : 
            if parents[neighbor] is not None: continue
            new.length = length + weights[(node, neighbor)]
            heapq.heappush(heap, (new_length, neighbor, node))
    # end while
    if parents[target] is None : return None, None
    path = [target]
    while path[-1] != start : path.append(parents[path[-1]])
    path.reverse()
    return path, length

Complexity of Dijkstra Shorteste Path

while len(heap) != 0:

In the heap we add edges, and we do not re-add edges multiple times. Therefore the number of iterations is $\mathcal{O}(|E|)$

heappop(): $\log{len(heap)} \Rightarrow \mathcal{O}(|E|)$:

in usual graphs (no multiedges): $|E| \in \mathcal{O}(|V|^2) = \mathcal{O}(\log({|V|})$

for neighbor: $\mathcal{O}(degree(node)) \in \mathcal{O}(|V|)$

$\Rightarrow$ overall complexity: $\mathcal{O}(|E|\log{|V|})$

Correctness of Dijkstra Shortest Path

Lemma: in the (i + 1)-st iteration of the while-Loop: $length_{i + 1} \geq length_{i}$
Proof (indirect, proof by contradiction): asssume $l_{i + 1} < l_i$ for some $i$. This means that $l_i$ was at the Top in the heap at the iteration $i$, $l_{i + 1}$ was at the top at the iteration $i+1$
- case 1: the path with the length $l_{i+1}$ was already known during the iteration $\Rightarrow$ $l_i$ could not have been top $\Rightarrow \quad \bot$
- case 2: path of length $l_{i + 1}$ was discovered during the itration $i$. Then we have $l_{i + 1} = l_i + W_{parent_i, node_i} > l_i$ $\Rightarrow \quad \bot$ $\Rightarrow l_{i + 1} < l_{i}$ is impossible.
Theorem: Dijstras response: $node \rightarrow parent \rightsquigarrow start$ is the shortest path from $node \rightsquigarrow start$, length $l_D$.

True shortest path: $node \rightarrow x \rightsquigarrow start$ with length $l_N < l_D$ shows that is impssible via a contradiction. we know who $(l_{D}, node, parent)$ at the top of the heap is
- case 1: $x \rightsquigarrow start$ is already in heap, if $w_{node, x} + len(x \rightsquigarrow start) = l_w < l_D$, would have been already found in an earlier iteration $\Rightarrow \quad \bot$
- case 2: $x

Notes

from collections import deque
import heapq

# gl = [[1,2], [0,3,4], [0,3,5,6], [1,2], [1], [2], [2]]
# g_cycle = [[1, 2], [0, 2], [0, 1]] 
# g_comp = [[1, 2], [0], [0], [4], [3]]

def transpose_graph(graph):
    gt = [[] for _ in graph]
    for node, neighbors in enumerate(graph):
        for nbr in neighbors:
            gt[nbr].append(node)
    return gt

def dfs(g, u):
    visited = set();
    def visit(v):
        if v in visited: return
        visited.add(v)
        print(f"discovered {v}")
        for neighbor in g[v]:
            visit(neighbor)
        print(f"finished {v}")
    visit(u)

def dfs_it(g, u):
    s = deque()
    s.append(u)
    visited = set()
    while s: # still node to be processed
        node = s.pop()
        if node in visited: 
            continue
        visited.add(node)
        print(f"discovered {node}")
        for neighbor in g[node]:
            if neighbor not in visited: # this line also can be omitted
                s.append(neighbor)


def dfs_it2(g, start):
    s = deque([start])
    visited = {start}   # mark root immediately
    while s:
        node = s.pop()
        print(f"discovered {node}")
        # reverse neighbors so the left-most neighbor is processed first
        for neighbor in reversed(g[node]):
            if neighbor not in visited:
                visited.add(neighbor)  # mark here (before pushing)
                s.append(neighbor)




def bfs_it(g, u):
    q = deque()
    q.append(u)
    visited = set()
    while q: # still node to be processed
        node = q.popleft()
        if node in visited: 
            continue
        visited.add(node)
        print(f"discovered {node}")
        for neighbor in g[node]:
            if neighbor not in visited: # this line also can be omitted
                q.append(neighbor)

def bfs_it2(g, u):
    q = deque([u])
    visited = {u}
    while q:
        node = q.popleft()
        print("discovered", node)
        for nbr in g[node]:
            if nbr not in visited:
                visited.add(nbr)
                q.append(nbr)

def bfs_dp(g, start):
    q = deque([start])
    dist = {start: 0}
    parent = {start: None}
    visited = {start}                 # mark on enqueue

    while q:
        u = q.popleft()
        # here u is being processed: dist[u] is its shortest distance
        print(f"processing {u} dist={dist[u]}")
        for v in g[u]:
            if v not in visited:
                visited.add(v)
                parent[v] = u
                dist[v] = dist[u] + 1
                q.append(v)

    return dist, parent


def dfs_dp(g, start):
    visited = set()
    q = deque([start])
    dist = {start: 0}
    parent = {start: None}

    while q:
        u = q.pop()
        if u in visited: continue
        visited.add(u)
        print(f"processing {u} dist={dist[u]}")
        for v in g[u]:
            if v not in visited:
                parent[v] = u
                dist[v] = dist[u] + 1
                q.append(v)

    return dist, parent


def reconstruct_path(parent, start, target):
    if target not in parent:
        return None
    path = []
    node = target
    while node is not None:
        path.append(node)
        if node == start:
            break
        node = parent[node]
    if path[-1] != start: 
        return None # we reached None before hitting start -> unreachable node
    path.reverse()
    return path

def copy_dfs(g, u):
    """
    copy the reachable component of `g` starting at `start` using DFS pre-order
    Returns (new_adj, mapping) where mapping maps old_index -> new_index
    """
    if u < 0 or u >= len(g): 
        return [], {}
    mapping = {}
    g_new = []
    s = [u]

    # assign start immediately (pre-order)
    mapping[u] = 0
    g_new.append([])

    while s:
        u = s.pop()
        # iterate neighbors (natural order); 
        for v in g[u]:
            if v not in mapping:
                mapping[v] = len(g_new)
                g_new.append([])
                s.append(v)
            g_new[mapping[u]].append(mapping(v))
    return g_new, mapping


def dfs_delete(g, start):
    """
    delete the reachable component of `g` starting at `start` using DFS post-order
    - Deletion here means: clear g[u] and remove u frm adjacency lists of all other nodes
    modifies g in-place. Returns list of deleted nodes (in the order they arrived)
    """

    n = len(g)
    visited = set()
    deleted = []
    def visit(u):
        if u in visited: 
            return
        visited.add(u)
        for v in list(g[u]): # iterate a copy, because we will modify on deletes
            visit(v)
        # post-order: now delete u
        # remove u from other adjacency lists
        for w in range(n):
            g[w] = [x for x in g[w] if x != u]
        # clear u's adjacency list
        g[u] = []
        deleted.append(u)
    visit(start)
    return deleted

def has_cycle(g):
    n = len(g)
    visited = set()

    def dfs(u, parent):
        visited.add(u)
        for v in g[u]:
            if v == parent: 
                continue
            if v in visited: 
                return True
            if dfs(v, u): return True
        return False

    # explore graph from
    return dfs(0, -1)

def connected_components_vl(graph) : # graph given as an adjecency list
    labels = [None] * len(graph)
    anchors = [None] * len(graph)


    def visit(node, anchor):
        if anchors[node] is not None: 
            return # already visited / known component
        labels[node] = labels[anchor]
        anchors[node] = anchor
        for neighbor in graph[node] :
            visit(neighbor, anchor)


    current_label = 0
    for node in range(len(graph)) :
        if labels[node] is not None: continue
        labels[node] = current_label
        visit(node, node) # a compnent is now complete
        current_label += 1
    return labels, anchors

def connected_components_dfs(g):
    n = len(g)
    labels = [-1] * n
    anchors = [None] * n

    def dfs(u, anchor, cid):
        """
        visit all nodes reachable from anchor, 
        assign them the component id `cid`, which is the label of the anchor
        assign their anchor as `anchor`
        """
        labels[u] = cid
        anchors[u] = anchor
        for nbr in g[u]: 
            if labels[nbr] == -1:
                dfs(nbr, anchor, cid)

    cid = 0
    for s in range(n): # loop over all nodes
        if labels[s] != -1:
            continue
        dfs(s, s, cid) # flood-fill component represented by s
        cid += 1
    
    return labels, anchors, cid

def connected_components_bfs(g):
    n = len(g)
    labels = [-1] * n
    anchors = [None] * n
    cid = 0

    for s in range(n):
        if labels[s] != -1:
            continue
        q = deque([s])
        labels[s] = cid
        anchors[s] = s
        while q:
            u = q.popleft()
            for v in g[u]:
                if labels[v] == -1:
                    labels[v] = cid
                    anchors[v] = s
                    q.append(v)
        cid += 1
    return labels, anchors, cid

def groups_from_labels(labels):
    comps = {}
    for i, c in enumerate(labels):
        comps.setdefault(c, []).append(i)
    # return components in label order
    return [comps[c] for c in sorted(comps)]

def shortest_path_vl(g, start, target): # graph is undirected
    """
    BFS on an unweighted (undirected) graph given as list-of-lists.
    Returns a list [start, ..., target] for a shortest path, or None if unreachable
    """
    n = len(g)
    if not (0 <= start < n and 0 <= target < n):
        return None
    if start == target:
        return [start]
    
    parent = [-1] * n               # -1 means undiscovered
    parent[start] = start           # root points to itself
    q = deque([start])

    while q:
        u = q.popleft()
        if u == target:
            break                   # early exit: target reached
        for v in g[u]:
            if parent[v] == -1:
                parent[v] = u
                q.append(v)

    if parent[target] == -1:
        return None                 # unreachable

    # reconstruct the path target -> ... -> start
    path = [target]
    while path[-1] != start:
        path.append(parent[path[-1]])
    path.reverse()
    return path



## topological sorting

def topological_sort(g):
    """
    input: `g` a directed acyclic graph with vertices numbered 0..n
    output: a linear order of the vertices s.t. u appears before  v in the linear
    order 
    """
    n = len(g)
    indeg = [0] * n                              # 
    # initialize in degree
    for u in range(n):
        for v in g[u]: 
            indeg[v] += 1


    # holds nodes with in-degree 0
    q = deque([v for v in range(n) if indeg[v] == 0])
    order = []

    while q:
        u = q.popleft()
        order.append(u)
        for v in g[u]: 
            indeg[v] -= 1
            if indeg[v] == 0:
                q.append(v)

    return order if len(order) == n else None


def dag_shortest_path(g, weight, s):
    """
    `g`: a weighted directed acyclic graph represented as list of lists, where 
    nodes are indexed 0 .. len(g) - 1
    `s`: start node
    `weights`: mapping of edge -> weight
    """
    n = len(g)
    INF = float("inf")

    shortest = [INF] * n
    shortest[s] = 0
    parent = [-1] * n

    def relax(u, v):
        if shortest[u] + weight[(u, v)] < shortest[v]:
            shortest[v] = shortest[u] + weight[(u, v)]
            parent[v] = u

    order = topological_sort(g)
    for u in order:
        if shortest[u] == INF:
            continue
        for v in g[u]:
            relax(u, v)

    return shortest, parent

# g_top = [[1, 2], [2], [3, 4, 5], [4, 5], [5], []]
# weights = {(0, 1):5, (0,2):3, (1,2):2, (2,3):7, (2,4):4, (2,5):2, (3,4):-1, (3,5):1, (4,5):-2}


def dijkstra(g, weight, s):
    """
    `g`: directed graph 
    `weight`: mapping of edge -> weight
    `s`: start node 
    output: 
    - `dist`: for each non-source vertex v in V, dist[v] is the weight of
    a shortest path from s to v and pred[v] is the vertex preceding on some shortest path
    """

    n = len(g)
    INF = float("inf")

    dist = [INF] * n
    dist[s] = 0
    parent = [-1] * n
    settled = [False] * n


    def relax(u, v):
        if dist[u] + weight[(u, v)] < dist[v]:
            dist[v] = dist[u] + weight[(u, v)]
            parent[v] = u

    pq = [(0, s)]

    while pq:
        d, u = heapq.heappop()
        if settled[u]:
            continue
        settled[u] = True

        for v in g[u]:
            nd = d + weight[(u, v)]
            if nd < dist[v]:
                dist[v] = nd
                parent[v] = u
                heapq.heappush(pq, (nd, v))

    return dist, parent



def dijkstra_gpt(g, weights, start, target=None):
    n = len(g)
    INF = float("inf")
    dist   = [INF]*n
    parent = [-1]*n
    settled = [False]*n

    dist[start] = 0.0
    parent[start] = start
    pq = [(0.0, start)]

    while pq:
        d, u = heapq.heappop(pq)
        if settled[u]:
            continue                   # stale entry for a node already finalized
        settled[u] = True              # first pop → distance to u is final

        if target is not None and u == target:
            break

        for v in g[u]:
            if settled[v]:
                continue
            nd = d + weights[(u, v)]
            if nd < dist[v]:
                dist[v] = nd
                parent[v] = u
                heapq.heappush(pq, (nd, v))

    if target is None:
        return dist, parent
    if not settled[target]:
        return None, None
    # reconstruct path
    path = []
    x = target
    while True:
        path.append(x)
        if x == start: break
        x = parent[x]
    path.reverse()
    return path, dist[target]



def prim_mst(gw, start=0):
    """
    gw: adjacency list where gw[u] = [(v, weight), ...] for an undirected graph.
    Returns (edges, total_weight) where edges are (u, v, w) in the MST.
    """
    n = len(gw)
    INF = float('inf')

    key     = [INF] * n      # cheapest edge weight connecting v into the tree
    parent  = [-1]  * n      # parent[v] = u that gives that cheapest edge
    in_tree = [False] * n

    key[start] = 0.0
    pq = [(0.0, start)]      # (key, vertex)
    edges = []

    while pq:
        k, u = heapq.heappop(pq)
        if in_tree[u]:
            continue
        in_tree[u] = True
        if parent[u] != -1:                 # skip root (no incoming edge)
            edges.append((parent[u], u, k)) # k == key[u]

        for v, w in gw[u]:
            if not in_tree[v] and w < key[v]:
                key[v] = w
                parent[v] = u
                heapq.heappush(pq, (key[v], v))

    total = sum(w for _, _, w in edges)
    return edges, total