Week 10

VL 19 - 17.06.25

Complexity / Depth of Anderson Trees (“AA-Tree”)

properties of anderson trees:

• 0: search-tree condition
• 1-3: horizontal edges
• 4: all nodes that are not at the lowest level, i.e. not the smallest sentinel distance, have exactly two children

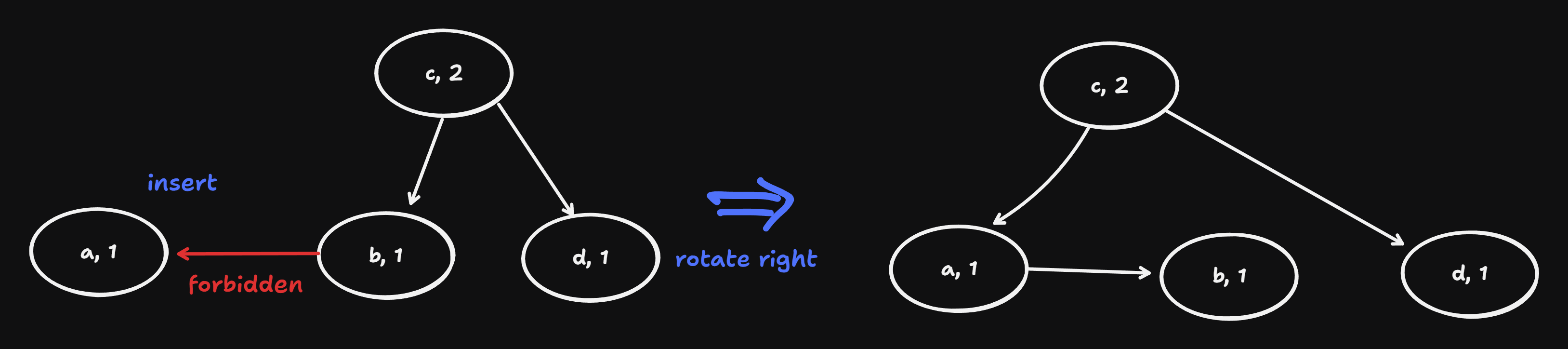
Main point idea of Anderson: 0-4 are by appropriate impelemntation of insert and remove always satisfiable.

Last if of insert:

if node.right is not None and node.right.right is not None and \
    node.dist == node.right.right.dist: # 
        node = rotate_left(node)
        node.dist += 1 # this node has two children, because in hte midle of the chain in the tree

Consequence for the depth:

• lowest level: k = k_min => N_min(k_min) = 1
• higher levels:
  • Case 1: no horizontal edge: N_min(k) = 1 + 2 N_min(k - 1)
  • Case 2: right horizontal edge: N_min(k) = 1 + N_min(k - 1) + 1 + 2 N_min(k - 1) = 2 + 3 N_min(k - 1)

Case 1 is corresponds exactly to the perfect tree, k = log_2(N + 1)

• Summary:
  • k_max <= log_2(N + 1) always holds (k_max is the distance to the root)
  • there are never two subsequent horizontal edges => d <= 2k_max
  • \(\Rightarrow\) d <= 2 log_2(N + 1) (basically same complexity as a perfectly balanced tree).

anderson-insert

Priority Search

• we search for a node with highest (max priority search) or lowest priority (min priority search) (not for a specific key)
• if we have max priority we can automatically can have a min priority searching by simply redefining the priority
  • priority -> -priority
  • priority -> 1 / priority
• applications:
  • job queues on a machine or a cpu
  • shortest paths in graphs
  • heapsort
  • stack (LIFO) and queue (FIFO): are special cases of priority queues / priority search: waiting_time := now - arrive_time
    • \(\Rightarrow\) queue: max priority search with waiting_time
    • \(\Rightarrow\) stack: min priority search with waiting_time

Simple Algorithms for finding the max Element

• sequential search in an array a: finding the max element (same as inner loop of selection sort)

  m = 0
  for i in range(1, len(a)):
    if a[i] > a[m]: m = i
    return m

• sorted array: m = len(a) - 1: O(1), but O(N log(N)) sorting expense. This is usually inefficient, becase many elements are dynamically coming and leaving the queue. This would require resorting

• search tree:

  node = root
  while node.right is not None:
    node = node.right
  return node

  same as tree_predecessor(node.left)

• but we can do better! \(\Rightarrow\) Heap Data Structure

Heap Data Structure

finding the max element is O(log(N)) but the constant within are better, also heaps can be stored as arrays instead of linked nodes as with search trees, which makes it even faster in practice.

• Heap is a binary tree with two properties:

  1. perfectly balanced and left-leaning (can be stored as an array)

     

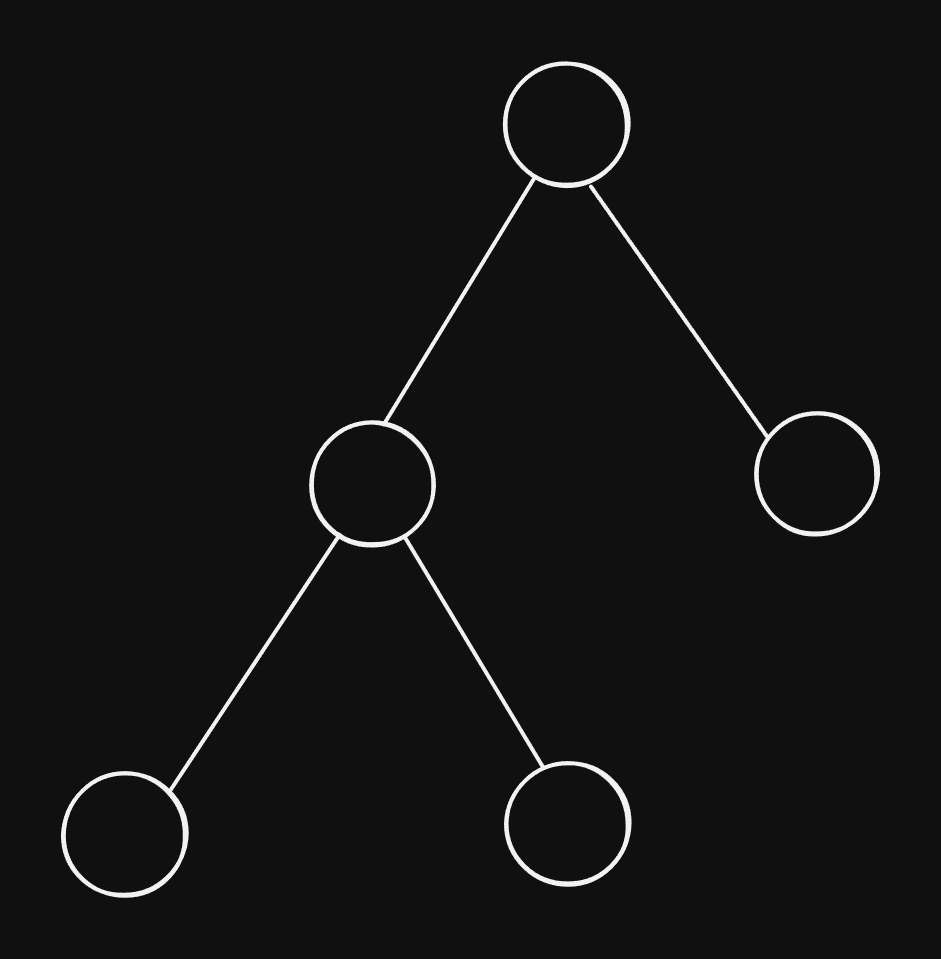
     heap-tree

  2. Heap-property: the root of every sub-tree has the highest priority in the sub-tree \(\Rightarrow\) largest element is the root of the whole tree.

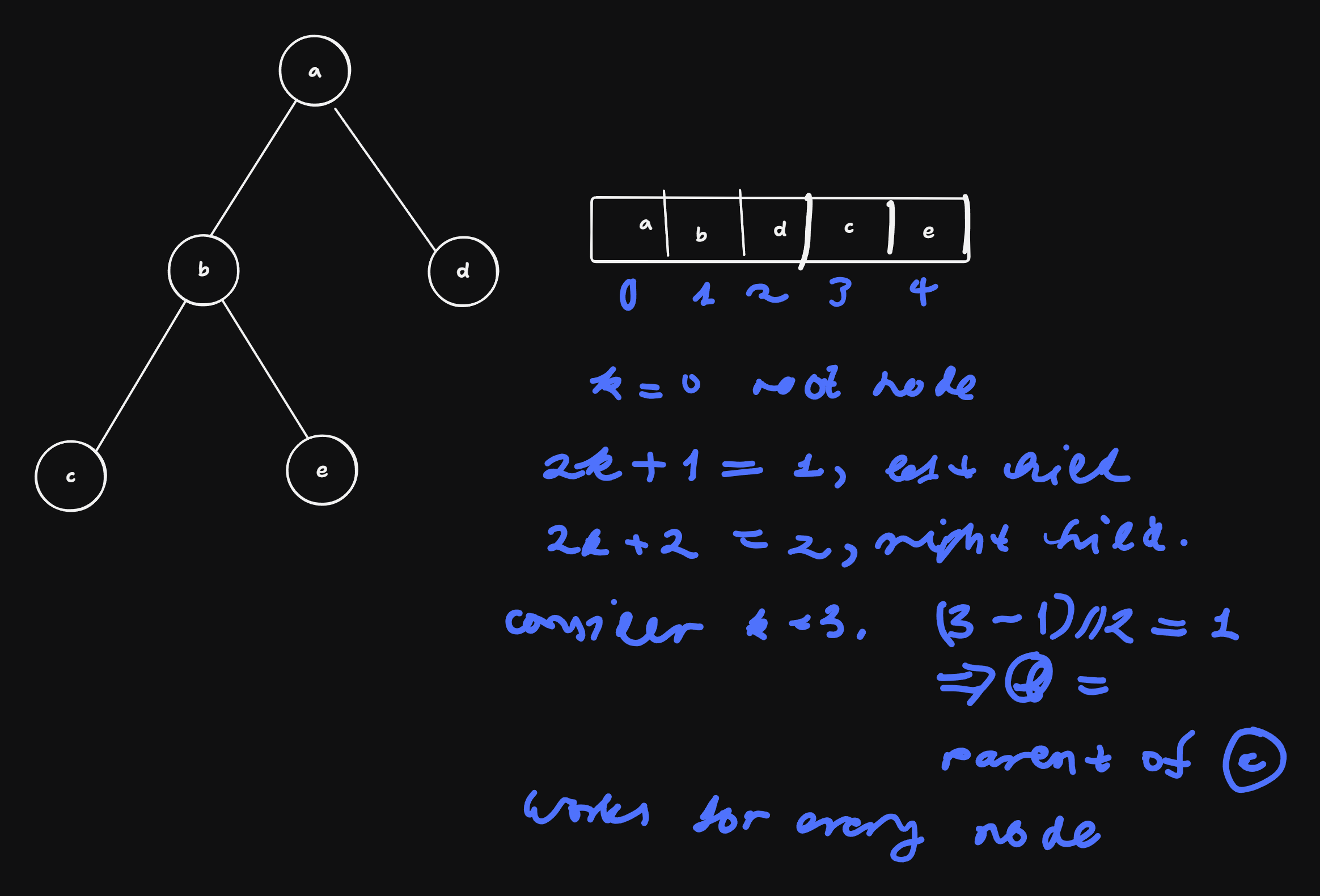
• flattening: representation of a left-leaning heap as array
  • nodes are stored level-wise one after the other:
    • child of k: 2k + 1 or 2k + 2
    • parent of k: (k - 1) // 2

flattening

Implementation of the Heap Data Structure

class Heap:
    def __init__(self): self.data = []
    def __len__(self): return len(self.data)
    def top(self): return self.data[0]
    def pop(self): # removes top
    def push(self, priority) # insert

• basic principle of insertion:

  1. new element is inserted at the end of self.data. (this is efficient due to amortized O(1) complexity of heap)
  2. swap elements until heap condition is satisfied again: O(log N)

• implementation:

  def push(self, priority):
    self.data.append(priority) # step 1
    upheap(self.data, len(self.data) - 1) # step 2, len(self.data) - 1 is the index of the last element, that is possibly at wrong position

  upheap() is what we must implement

  def upheap(a, k): 
    v = a[k] # intermediately store the element k, priority of k
    while True: # infinite loop, left with break
        if k == 0: # top node, can't go higher => break
             break
        parent = (k - 1) // 2
        if a[parent] > v: # heap condition is satisfied
            break
        a[k] = a[parent]
        k = parent
    a[k] = v